Introducción
El insumo de la estadística tanto descriptiva como inferencial es la información, por lo que la obtención de la muestra juega un papel central en la validez de los resultados. En estadística inferencial, con los valores recabados en una muestra, se puede deducir el valor de un parámetro de interés, lo que permitirá determinar el comportamiento de una población.
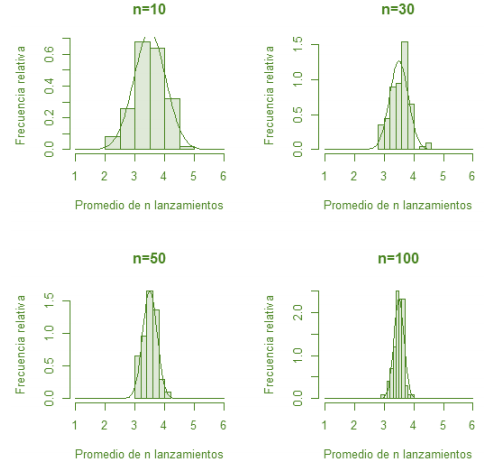
De tal forma que en este tema se expondrá uno de los resultados más importantes de la teoría de la probabilidad: el teorema del límite central.
En el ámbito empresarial y de los negocios, no siempre es posible contar con la información de toda una población, por lo que se tiene que recurrir a la estadística inferencial y, en particular, al teorema del límite central, el cual nos garantiza la representatividad de la población objeto de estudio.
¡Comencemos!

Altmann, G. (2016). Grupo [ilustración]. Tomada de https://pixabay.com/es/icono-persona-grupo-personas-1250084/
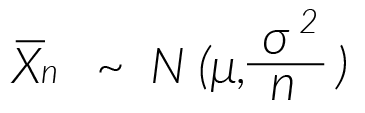
 : promedio de n variables
: promedio de n variables : distribución normal con media µ y varianza σ2/n
: distribución normal con media µ y varianza σ2/n![(s. a.) (2017). Juego de mesa [fotografía]. Tomada de https://pxhere.com/es/photo/893719](img/3_dados.jpg)