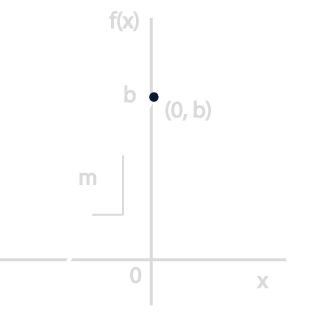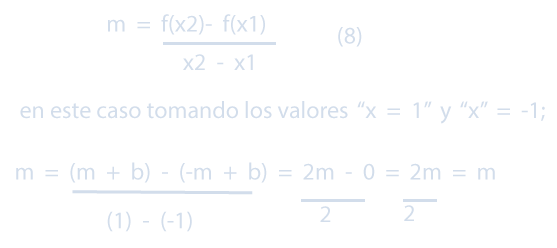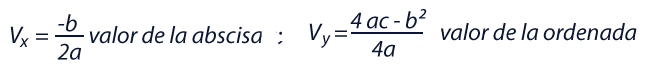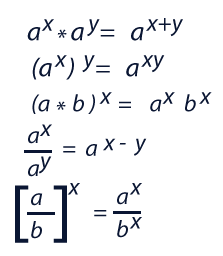Funciones

Unidad de Apoyo para el Aprendizaje

Iniciar

Introducción


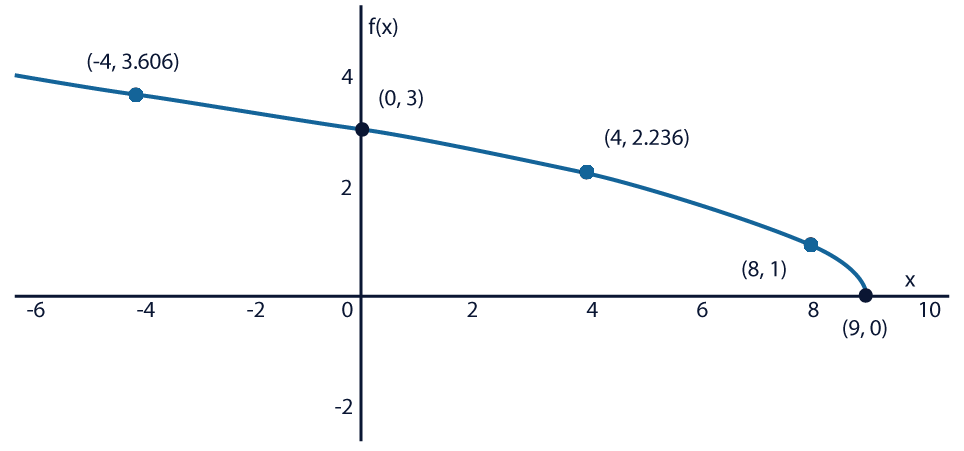
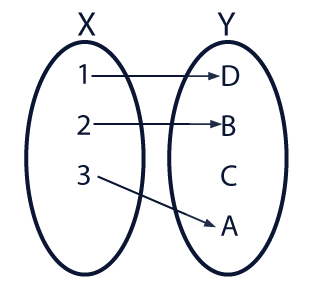
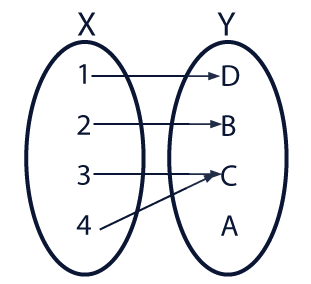
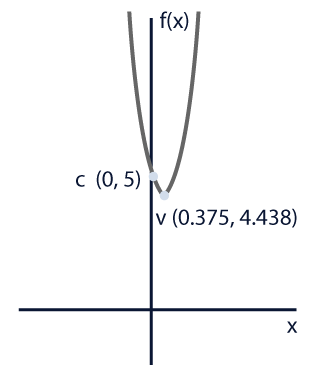
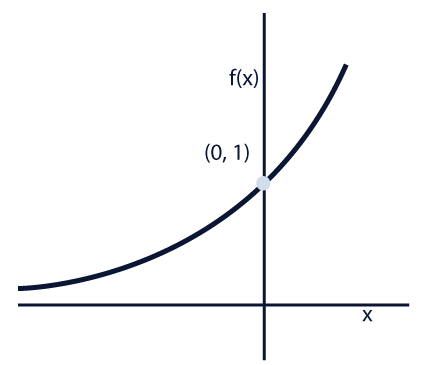
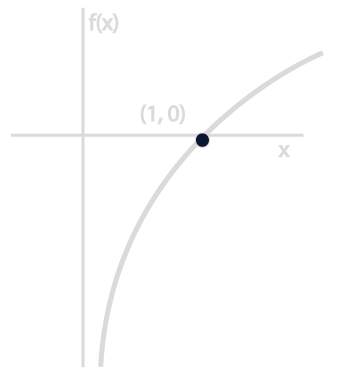
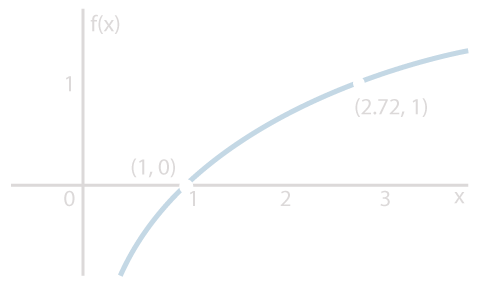
Observa las siguientes imágenes:



¿Cómo crees que se relacionan?

El origen del cálculo puede ubicarse en varios escenarios, desde la Grecia Antigua hasta los planteamientos que desarrolló Isaac Newton en sus estudios del movimiento. A Newton se le considera el creador del cálculo diferencial e integral, ya que fue el primero en plantear y desarrollar los elementos que permiten diferenciar esta disciplina del álgebra; en su texto Methodus Fluxiorum et Serierum Infinitorum (1671), se puede ubicar claramente el uso de variaciones infinitesimales relacionadas con el surgimiento formal del cálculo diferencial; en De Analysi (1669), empiezan a vislumbrarse elementos del cálculo integral.

En estas obras sobre el estudio de la mecánica, Newton concibe las cantidades matemáticas como el movimiento continuo de un punto que traza una curva, y enuncia: “Cada una de estas cantidades donde aparecen variables ‘x’ es un fluente y su velocidad, designada por ‘x’, es una fluxión. La parte infinitesimal pequeña donde un fluente se incrementa por unidad de tiempo cero es el momento del fluente. El problema fundamental es, dada una relación entre fluentes, hallar la relación entre sus fluxiones y recíprocamente”.

El significado de estos textos implica llegar a los conceptos de límite y función que Newton enuncia a continuación de esta manera: “Por última proporción de cantidades evanescentes debemos entender el cociente de estas cantidades, no antes de que desvanezcan, ni después, pero tal como van desvaneciendo. La parte infinitesimal pequeña donde un fluente se incrementa por unidad de tiempo cero es el momento del fluente. El problema fundamental es, dada una relación entre fluentes, hallar la relación entre sus fluxiones y recíprocamente”.







Fluxiones de Isaac Newton.

Fluxiones de Isaac Newton



Analizar el concepto de función a través de su origen, sus variantes y técnicas para su diagramación.

Origen del concepto de función


Así como Newton requiere enunciar a través de los fluentes una relación de dependencia matemática entre dos variables y por medio de ellas abordar las cantidades evanescentes, será conveniente revisar el concepto de función.



Una imagen de algoritmos con pequeñas siluetas de personas

(s. a.) (s. f.). Sir Isaac Newton [pintura]. Tomada de https://commons.wikimedia.org/wiki/File:Sir_Isaac_Newton.jpgv

Relaciones y funciones


Una relación matemática (R) es la correspondencia que existe entre dos conjuntos dados a un elemento del primer conjunto (llamado dominio), al cual le corresponde al menos un elemento del segundo conjunto (denominado contradominio).



Sin embargo, en la visión de cambio propuesta por Newton se da en un continuo, en partes infinitesimales, y requiere relacionar los fluentes (variables) con sus cambios (regla de correspondencia) de manera recíproca.

De esta forma, la idea de relación en matemática es abierta en la forma en que se pueden relacionar las variables (al menos un elemento del segundo conjunto); esta posibilidad evita una aplicación directa del concepto de relación matemática ante la necesidad que Newton tiene, la cual expresa “cómo un fluente se incrementa por unidad de tiempo y de manera recíproca”, es decir, requiere de manera específica un tipo de relación acotada “uno a uno” donde no quede duda, ya que una relación puede ser uno a varios. Por ello, es necesario formalizar este tipo de relación única, es decir, unívoca, ya que de esta manera sólo acepta un significado, lo cual explica la aparición del concepto de función.

Definición de función matemática


De lo anterior, es posible enunciar lo siguiente:

Una función, denotada como f(), es una regla de correspondencia que asocia a cada elemento “x” de un primer conjunto denominado dominio con un solo elemento (f(x)) de un segundo conjunto denominado contradominio; esto implica que, dados dos diferentes elementos (x1 y x2) del dominio, entonces la regla de correspondencia asignará en el contradominio un f(x1) que es diferente de f(x2).



Por ende, es pertinente indicar que una función es un tipo especial de relación matemática y todas las funciones son relaciones, pero no todas las relaciones son funciones.

En la siguiente figura se ilustra el concepto:



Función matemática

Función matemática

Ecuaciones y funciones


Una vez determinado el concepto de función, ahora se mostrará su aplicación en la matemática, sobre todo para una ecuación dada.

Recuerda que, por sí misma, una ecuación establece de manera general una relación matemática; esto se observa de manera más específica al considerar que, a la derecha del signo de igualdad (=), se tienen los elementos del dominio (las “x”), la regla de correspondencia (f( )) dada por la operación u operaciones que se indican en este lado de la igualdad y los elementos del contradominio que se muestran en el otro lado (izquierdo).

Para aclarar este planteamiento, se muestra a continuación un caso específico de ecuación en torno al concepto de función. Revisa el siguiente ejemplo y pulsa las flechas para avanzar y retroceder por la información.



Tipos de funciones


A partir del concepto de función, se sabe que éste consta de una regla de correspondencia, pero en toda función también están involucrados dos conjuntos, uno denominado dominio y otro llamado contradominio; en ocasiones, a partir del planteamiento de un problema de inicio se proponen estos dos conjuntos y, bajo este enfoque, se dice que una función puede clasificarse en tres diferentes tipos que se muestran a continuación.

Función inyectiva

Se trata de una función inyectiva si a diferentes elementos "x" del dominio les corresponden diferentes elementos "y" del contradominio.



Considera una función a través de una ecuación como la siguiente:

s Y = 2x (4)

Ejemplo de función inyectiva

Ejemplo de función inyectiva



Al estipular que el dominio y contradominio son el conjunto de los números naturales, entonces el dominio quedará cubierto en su totalidad {1, 2, 3…}, mientras el contradominio sólo comprenderá los números naturales pares {2, 4, 6…}, es decir, hay elementos del contradominio propuesto que no quedan cubiertos por la regla de correspondencia.

Función suprayectiva

Se trata de una función suprayectiva cuando cada elemento de “Y” es imagen de por lo menos, un elemento de “X” del dominio.



y = |x| (5)



Ejemplo de función suprayectiva

Ejemplo de función suprayectiva



Aquí se observa que, al tomar todos los números enteros ({…, -2, -1, 0, 1, 2,…}) para el dominio y contradominio, entonces en el contradominio se tendrán solamente los números enteros positivos {0, 1, 2…}, es decir, se requieren menos elementos en el contradominio propuesto para cubrir todos los elementos del dominio de acuerdo con la regla de correspondencia.

Función biyectiva

Todos los elementos del conjunto del dominio tienen una imagen distinta en el conjunto del contradominio.



y = x (6)



Ejemplo de función suprayectiva

Ejemplo de función suprayectiva



Aquí se observa que, al tomar los números enteros {…, -2, -1, 0, 1, 2,…} para el dominio, la relación es idéntica {…,-2, -1, 0, 1, 2,…} en el codominio o contradominio, es decir, se requieren tantos elementos en el dominio como en el contradominio de acuerdo con la regla de correspondencia.

Es importante notar que estas clasificaciones se verán afectadas según la forma en que se establecen los conjuntos que son parte de la definición de una función; en estos casos, la regla de correspondencia juega el papel de fiel de la balanza en su clasificación.

Funciones comunes


Ahora se hará una introducción a algunas funciones comunes en el planteamiento de problemas prácticos relacionados con el cálculo diferencial; por ello, es de utilidad conocerlas. Adicionalmente, esto facilitará la interpretación de conceptos como límite y derivación, los cuales se revisarán posteriormente. La clasificación propuesta refiere sus nombres a la representación geométrica de las funciones en el plano cartesiano.

Función lineal y su representación geométrica


Las ecuaciones que caen dentro de esta clasificación son aquéllas que matemáticamente tienen la siguiente forma:



En tanto, en su interpretación real se pueden asociar a las relaciones de proporcionalidad directa que aparecen en el planteamiento de un problema.

Al retomar la representación cartesiana por medio de coordenadas, se tiene que esta función tiene como dominio todos los valores posibles de “x”, ya que la multiplicación (por “m”) está permitida para cualquier valor numérico. Por ello, de igual forma el contradominio podrá tomar cualquier valor numérico de acuerdo con la regla de correspondencia y su lugar geométrico quedará determinado por medio de la coordenada genérica (x, (mx+b)), lo cual se muestra sintéticamente en la siguiente tabla:

x f(x) Coordenada
1 m + b (1, m + b)
0 b (0, b)
-1 -m + b (-1, -m + b)

Tabla 1. Tabulación de valores de la ecuación (7)



Como viste en el tema “Graficación de ecuaciones”, para trazar una línea recta se requieren solamente dos coordenadas; sin embargo, para enfatizar la función del parámetro “b”, se tabula y grafica de manera explícita, como se muestra en la siguiente figura:



Función lineal, gráfica y parámetros “m” y “b” de la ecuación f(x) = mx + bv

Función lineal, gráfica y parámetros “m” y “b” de la ecuación (7)



El valor “b” se denomina ordenada al origen y se asocia a la coordenada (0,b) o punto donde la recta intersecta al eje “f(x)” (o “y” de manera genérica en los ejes cartesianos), en tanto que el parámetro “m” se asocia a la pendiente de la recta (inclinación) y su valor puede obtenerse al realizar el cociente de la diferencia de ordenadas a la diferencia de abscisas, como se muestra a continuación:



Cálculo del parámetro “m”, pendiente de la función lineal de la ecuación f(x) = mx + b

Cálculo del parámetro “m”, pendiente de la función lineal (7)



Función cuadrática y su representación geométrica


Las ecuaciones que caen dentro de esta clasificación son aquéllas que matemáticamente tienen la siguiente forma:



Esta ecuación representa lo que matemáticamente se define como parábola, es decir, una de las curvas cónicas obtenidas mediante el uso de un plano como elemento de corte aplicado a un par de conos encontrados en sus vértices al considerar que el plano de corte se va girando en su acción.



Lo anterior se ilustra a continuación:

Obtención de las curvas “cónicas” a partir de un plano y dos conos encontrados en el vértice

Obtención de las curvas “cónicas” a partir de un plano y dos conos encontrados en el vértice



En la parte real, su nombre puede asociarse a su raíz etimológica, referente al análogo físico de arrojar un objeto que, en su trayectoria, describe una curva como la ilustrada en la parte derecha de la figura superior, o también relacionada al cálculo del área de un cuadrado.

A continuación, se muestran algunos parámetros de interés.



El signo del coeficiente “a” indica si la parábola “abre” en el sentido positivo o negativo del eje de las ordenadas. Esto es, si “a” es positivo, la gráfica abre en el mismo sentido de las ordenadas (cono superior); sí es negativo, la parábola “abre” en el mismo sentido (-) de las ordenadas (cono inferior), como se ilustra en la imagen de esta sección de cónicas a la derecha.

Es la mínima coordenada (o máxima dependiendo de la apertura), dentro del lugar geométrico de la parábola, su coordenada se obtiene por medio de las siguientes ecuaciones:



Este valor de la coordenada se obtiene al tomar el valor de “x” igual a cero.

Ejemplo

Determinar la apertura, vértice, punto de corte y gráfica de la siguiente parábola:

f (x) = 4x2 - 3x + 5

Revisa cada parámetro para conocer la solución al ejemplo anterior.

Solución

Apertura

Se da por el valor de “a” (4); al ser un número positivo, señala que la parábola abre hacia la parte positiva del eje de las ordenadas.



Vértice

Al sustituir los valores de “a” (4), “b” (-3) y “c” (5) en la ecuación (10):

Vx = -(-3) / 2(4) = 0.375 Vy = 4(4)(5) - (-3)2 / (4) = 4.438

Coordenada del vértice: V (0.375,4.438)

Corte con el eje de las ordenadas

Al hacer x = 0, de la ecuación propuesta se tiene lo siguiente:

4(0)2 - 3(0) + 5 = 5

Coordenada del punto de corte con el eje de las ordenadas: (0,5)

La gráfica y los parámetros desarrollados se muestran a continuación:

Es conocido también como autoimagen y es una compleja imagen que las personas tenemos de nosotros mismos.



Gráfica del ejemplo 4x2 - 3x + 5

f (x) = 4x2 - 3x + 5


Figura 9. Gráfica del ejemplo 2



Función polinomial y su representación geométrica


Las ecuaciones que caen dentro de esta clasificación son aquéllas que matemáticamente tienen la siguiente forma:

f(x) = anxn + an-1xn-1 + …a1x + a0            (11)
“ai” son constantes, n ∈ naturales



Su relación práctica con los problemas puede observarse en el caso de realizar una aproximación a una curva o serie de datos cuya ecuación que los describe no se conoce.

Este tipo de expresiones es una composición de potencias de la variable “x” y sus gráficas toman formas elaboradas; un comportamiento de interés se asocia a los valores de “x” donde la ecuación del polinomio corta el eje de las abscisas (y = 0), así como en la potencia máxima de “x” que aparece en la expresión y determina lo que se denomina el grado del polinomio; a continuación, se ilustra el caso de la ecuación:



f(x) = 3x5 - 5x4 - 5x3 + 5x2 - 0.2



Grado del polinomio: Está dado por la mayor potencia de “x”, en este caso, grado = 5.



Gráfica del polinomio de grado 5: 3x5 – 5x4 - 5x3 + 5x2 - 0.2

Gráfica del polinomio de grado 5: 3x5 - 5x4 - 5x3 + 5x2 - 0.2; el hecho de que no aparezca un término de la potencia (en este caso a1x1) no afecta su clasificación; se indican en color negro las coordenadas donde el polinomio corta el eje de las abscisas

Función exponencial y su representación geométrica


Las ecuaciones que caen dentro de esta clasificación son aquéllas que matemáticamente tienen la siguiente forma:





En estas ecuaciones, al valor “a” se le denomina base y a “x” exponente; este tipo de ecuaciones tienen un interés práctico debido a que se relacionan con el crecimiento de poblaciones y evolución financiera (entre muchos otros eventos de las ciencias sociales, exactas y naturales) y se representan por ecuaciones que muestran esta forma matemática.

Un punto de interés en este tipo de ecuaciones se da respecto al punto de corte con el eje de las ordenadas, ya que siempre se presenta para el valor “x” igual a cero, sin importar el valor de la base; por ello, la ubicación cartesiana para esta abscisa en todas las curvas se completa con la ordenada “y” igual a uno. De esta forma, se define la coordenada (0,1) para todas las ecuaciones de este tipo, como se muestra a continuación en una gráfica que ilustra el comportamiento general de este tipo de funciones:



Ilustración del corte con el eje de las ordenadas para todas las ecuaciones de tipo exponencial, ax

Ilustración del corte con el eje de las ordenadas para todas las ecuaciones de tipo exponencial (ax)



A continuación se listan algunas propiedades algebraicas de interés para este tipo de expresiones matemáticas:



Propiedades algebraicas para las ecuaciones exponenciales

Cuadro 1. Propiedades algebraicas para las ecuaciones exponenciales



Función logarítmica y su representación geométrica


Las ecuaciones que caen dentro de esta clasificación son aquéllas que matemáticamente tienen la siguiente forma:



El subíndice “a” de la ecuación nos indica la base donde se realizará la operación indicada por la ecuación. La utilidad práctica de este tipo de ecuaciones es a partir de las ecuaciones exponenciales, y se relaciona con la determinación del valor exponente donde la ecuación analizada arroja un resultado de interés, esto es, a través de ellas se puede saber en qué valor “x” la ecuación f(x) = ax (con “a” conocida) toma un valor específico.

Un comportamiento de interés para este tipo de ecuaciones alude al punto de corte con el eje de las abscisas y siempre se da para el valor x = 1, y la ubicación cartesiana para este valor de “x” en todas las curvas lo da la coordenada (1,0), como se muestra a continuación en una gráfica que ilustra el comportamiento general de este tipo de funciones.



Corte con el eje de las abscisas para todas las ecuaciones de tipo logarítmico, f(x) = loga(x), con x = 1, sin importar el valor de la base “a”

Corte con el eje de las abscisas para todas las ecuaciones de tipo logarítmico, f(x) = loga(x), con x = 1, sin importar el valor de la base “a”



Otro elemento de interés sobre este tipo de ecuaciones es que facilita la realización de diversos cálculos algebraicos y aritméticos, lo cual se observa directamente del cuadro que se proporciona a continuación:



Propiedades generales de los logaritmos, independientemente de la base “a”.

Cuadro 2. Propiedades generales de los logaritmos, independientemente de la base “a”



Ilustración de la primera propiedad de los logaritmos.

Ilustración de la primera propiedad de los logaritmos. El logaritmo de la base siempre es igual a 1, como se muestra en la coordenada de la derecha de la gráfica superior, ilustrada en color gris para el valor 2.72…, número irracional “e”, base de los logaritmos naturales



Conclusión


Aparentemente es sencilla la definición del concepto de función; sin embargo, éste se encuentra finamente entretejido en todas las demás ideas del cálculo diferencial; por lo tanto, su importancia no debe disminuirse, algo que comúnmente se hace, pues ya lo decía Isaac Newton: “El problema fundamental es, dada una relación entre fluentes, hallar la relación entre sus fluxiones recíprocamente”. Entonces, es esencial entenderlo y aplicarlo correctamente.

Actividad. Relación o función, evaluación de las características de una ecuación

En la aplicación práctica del cálculo diferencial, es de suma importancia poder enunciar las características funcionales de una ecuación para aplicar correctamente los conceptos de la disciplina.

Para esta actividad, considera la siguiente:


Autoevaluación. El concepto de función y su contexto

El concepto de función es uno de los pilares del cálculo diferencial; por ello, es importante conocer sus características, tipos y expresiones más comunes que permiten abordar problemas prácticos más complejos.

Fuentes de información

Básicas

Bibliografía Baldor, A. (1976a). Capítulo 30. En Álgebra. México: Publicaciones Cultural.

Baldor, A. (1976b). Capítulo 38. En Álgebra. México: Publicaciones Cultural.

Documentos electrónicos García, P. (s. f.). Funciones Inyectiva. Suprayectiva y Biyectiva (manuscrito no publicado) [Versión electrónica]. Facultad de Ingeniería-UNAM. Consultado el 3 de noviembre de 2017 de http://www.ingenieria.unam.mx/~colomepg/CAPITULO_I_FUNCIONES_III.pdf

Sitios electrónicos

Disfruta las Matemáticas. (2011). Sección: Inyectivo, Sobreyectivo y Biyectivo. Consultado el 3 de noviembre de 2017 de http://www.disfrutalasmatematicas.com/conjuntos/inyectivo-sobreyectivo-biyectivo.html

El descubrimiento del cálculo. (2002). Consultado el 3 de noviembre de 2017 de https://www.uam.es/personal_pdi/ciencias/barcelo/histmatem/calculo/calculo.html

Complementarias

Bibliografía Ayres, F. (1980). Cálculo Diferencial e Integral. México: McGraw-Hill.

Cómo citar

Garcés, A. M. (2017). Funciones. Unidades de Apoyo para el Aprendizaje. CUAED/Facultad de Contaduria y Administración-UNAM. Consultado el (fecha) de (vínculo)